The challenge of predicting creep-rupture life (CRL) for high-temperature alloys and specialty steels remains critical for designing turbojet engines, turbines, chemical and nuclear reactors, steam boilers, and other power equipment. This issue boasts a long history and a vast body of literature. The difficulty in addressing it stems from the immense complexity of microphysical mechanisms driving long-term strength degradation in modern steels and alloys under creep conditions.
Numerous traditional CRL prediction methods, rooted in the theory of thermally activated processes, fall short of delivering reliable results. These include the well-known time-temperature parametric method by F. R. Larson and J. Miller, proposed in 1952, alongside roughly 100 similar parameters. In the late 1970s, a team led by R. M. Goldhoff refined this approach, introducing the Minimum Commitment Method, endorsed for use in the USA. Typically, the extrapolation power of these methods - defined as the ratio of predicted time-to-rupture to maximum test time - rarely exceeds approximately 20.
Traditional prediction equations generally incorporate several empirical coefficients, tailored to specific material classes and test conditions. Determining these coefficients for each material demands extensive preliminary experimental and analytical effort.
In contrast, our new approach eliminates such pre-set coefficients entirely. This unlocks its potential for developing novel materials without analogs.
Our method is based on a refined version of a recognized phenomenological theory, viewing creep-induced rupture as the gradual accumulation of diffused damage - micropores and microcracks - over time. While conventional damage accumulation models assume linear summation under non-stationary loads, our approach introduces a more realistic and versatile nonlinear damage summation principle.
This method, paired with its algorithmic implementation, closely mirrors the actual kinetics of damage accumulation. It ensures highly certain CRL predictions with an extrapolation power exceeding two orders of magnitude beyond the maximum test time, driving significant savings in testing time, labor, and costs when developing new high-temperature metallic materials or assessing existing ones. Practically, standard CRL test results from durations of 1 to 4 (or up to 6) months yield reliable predictions spanning 10 to 40 years.
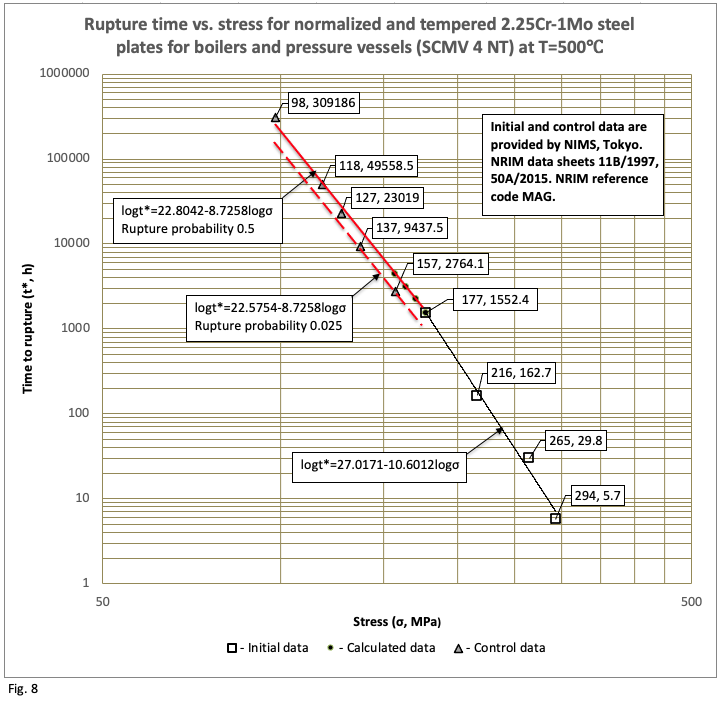
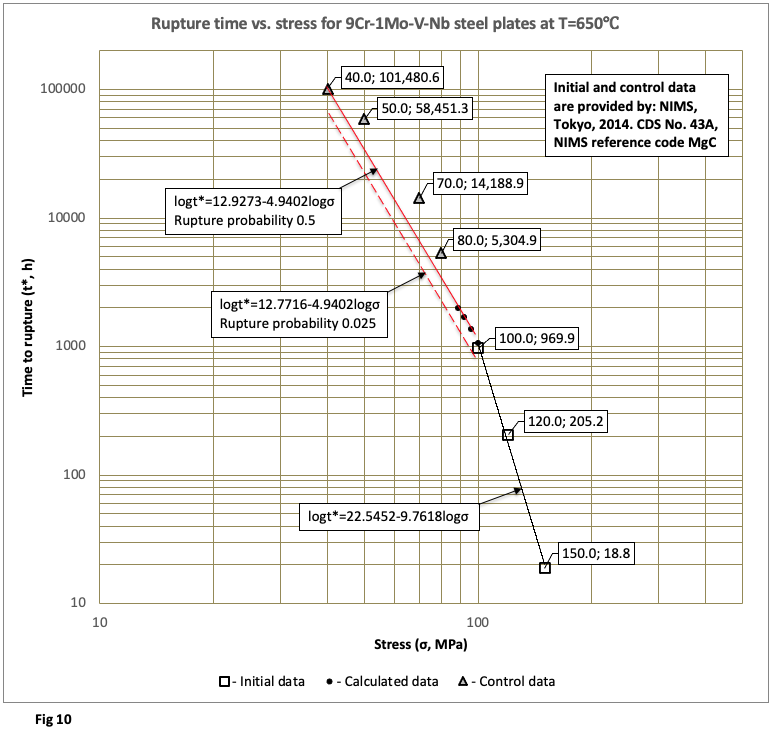
The method requires some time-limited results of standard creep rupture tests at a given constant temperature. These results, expressed as pairs of values (σ – t*), where σ is stress and t* is time-to-rupture, serve as the only essential input for subsequent calculations. The calculation process, grounded in the method’s theory, blends classical and modern statistical techniques to produce time-to-rupture predictions for relatively low-stress levels. Predictions cover both median rupture probability (p ≈ 0.5) and low-probability scenarios (e.g., p ≈ 0.025), with the option for detailed material survival analysis if needed.
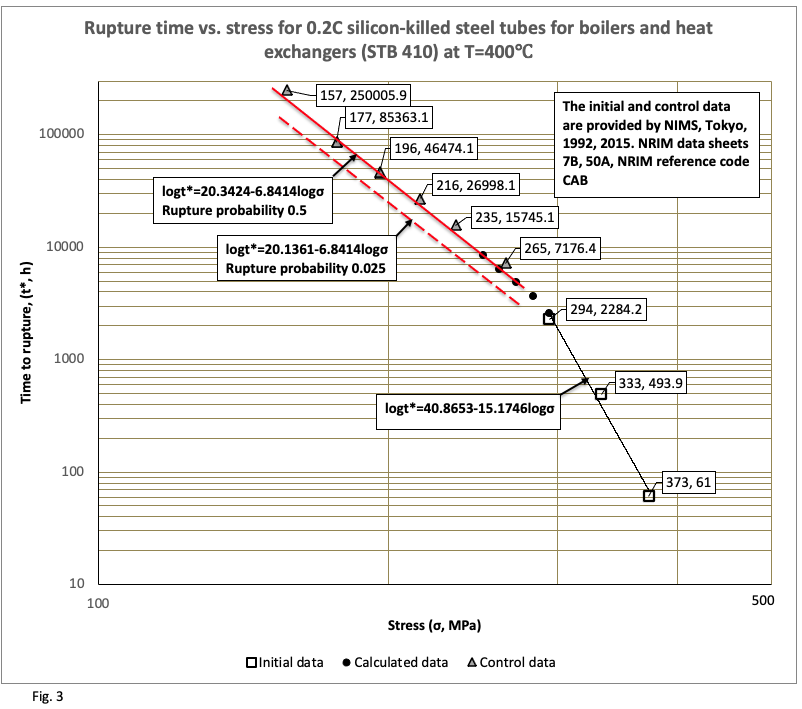
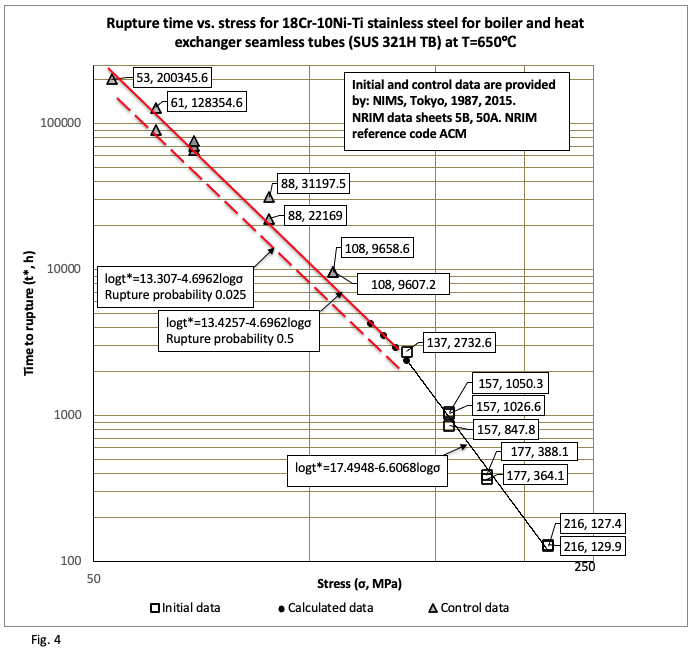
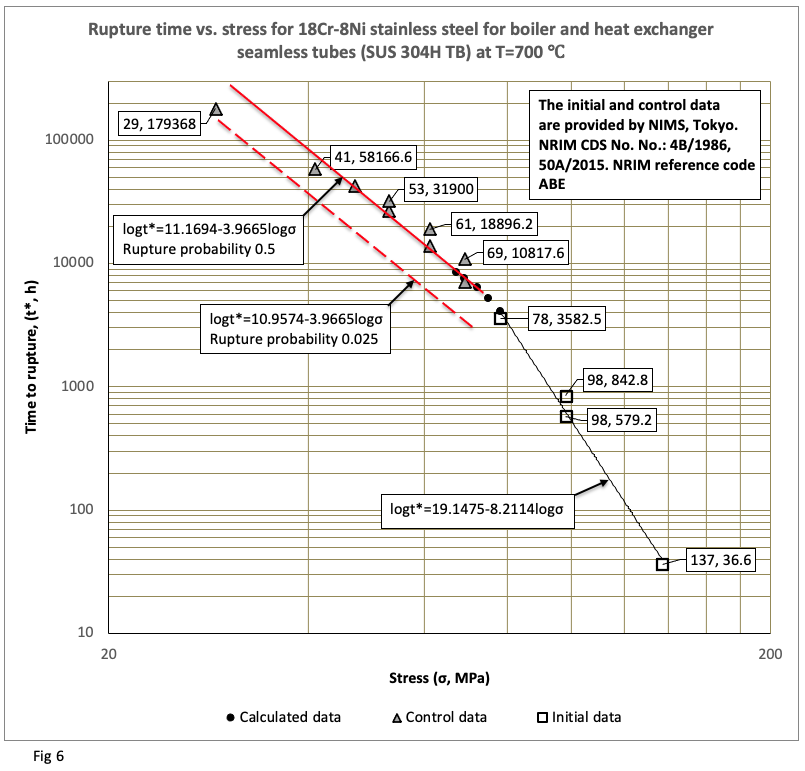
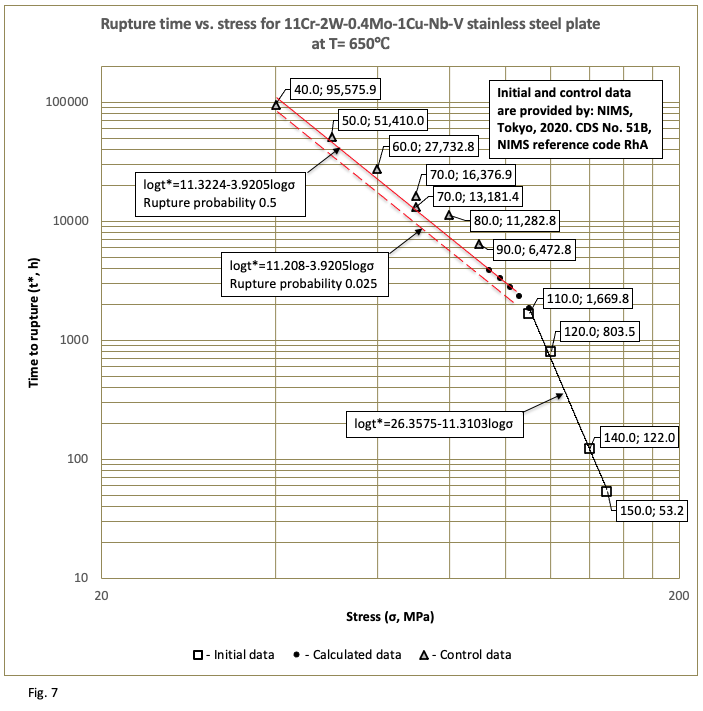
Examples of results, derived from applying the method across diverse materials and test conditions, appear in Figures 1 through 10: